Table of Contents
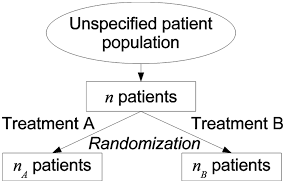
Randomization
“As per the National Cancer Institute “In research, the process by which participants in clinical trials are assigned by chance to separate groups that are given different treatments or other interventions.
Neither the researcher nor the participant chooses which treatment or intervention the participant will receive.
Using chance to assign people to groups means that the effects of the treatment or intervention that participants receive can be compared more fairly.”
Randomization is the process of making something random; in various contexts this involves, for example:
- generating a random permutation of the sequence (such as when shuffling cards);
- selecting a random sample of the population (important in statistical sampling);
- allocating experimental units via random assignment to the treatment or control condition;
- generating random numbers (see Random number generation); or
- transforming data stream (such as when using a scrambler in telecommunications).
What are the Reasons for Randomization?
Researchers in life science research demand randomization for a number of reasons.
First, topics in different groups do not vary in any systematic way. Within a clinical research, if patient groups are significantly different, research results will be biased.
Suppose that subjects are assigned to control and treatment groups in a study investigating the effectiveness of a surgical intervention.
If a greater proportion of the older subjects are assigned to the treatment group, then the result of the surgical intervention may be influenced by this imbalance.
The effects of the treatment would be identical from the influence of the imbalance of covariates, thereby requiring the researcher to control for the covariates in the analysis in order to obtain an unbiased result.
Second, proper randomization ensures no former knowledge of group assignment (i.e., allocation concealment). That is, researchers, subject or patients or participants, and others should not know to which group the subject will be assigned.
Knowledge of the group assignment creates a layer of potential selection bias that may taint the data.
Schul and Grimes stated that trials with insufficient or unclear randomization tended to overestimate treatment effects up to 40% compared with those that used proper randomization. The outcome of the research can be negatively influenced by this insufficient randomization.
Statistical techniques such as analysis of covariance (ANCOVA), multivariate ANCOVA, or both, are often used to adjust for covariate imbalance in the analysis stage of the clinical research.
On the other hand, the interpretation of this post adjustment approach is often difficult because imbalance of the covariates regularly leads to unanticipated interaction effects, such as unequal slopes among subgroups of covariates.
One of the critical assumptions in ANCOVA is that the slopes of the regression lines are the same for each group of the covariates.
The adjustment needed for each covariate group may vary, which is difficult because ANCOVA uses the average slope across the groups to adjust the outcome variable.
Thus, the ideal way of balancing covariates among groups is to apply sound randomization in the design stage of the clinical research (before the adjustment procedure) as an alternative of the post data collection.
In such instances, random assignment is essential and guarantees validity for the statistical tests of significance that are used to compare treatments.
What the types of Randomization?
Many procedures have been proposed for the random assignment of the participants to treatment groups in clinical trials.
Common randomization techniques includes, simple randomization, block randomization, stratified randomization, and covariate adaptive randomization, are reviewed.
Each method is described along with its advantages and disadvantages. It is very important to select a method that will produce interpretable and valid results for your study.
Use of online software to generate randomization code using block randomization procedure will be presented.
Simple randomization
Randomization based on a single sequence of the random assignments is known as simple randomization.
This technique maintains complete randomness of the assignment of a subject to a particular group.
The most common and basic method of the simple randomization is flipping a coin.
For example, with two treatment groups (control versus treatment), the side of the coin (i.e., heads – control, tails – treatment) determines the assignment of each subject.
Other methods include using shuffled deck of cards (e.g., even – control, odd – treatment) or throwing a dice (e.g., below and equal to 3 – control, over 3 – treatment).
A random number table found in a statistics book or computer-generated random numbers can also be used for the simple randomization of subjects.”
Block randomization
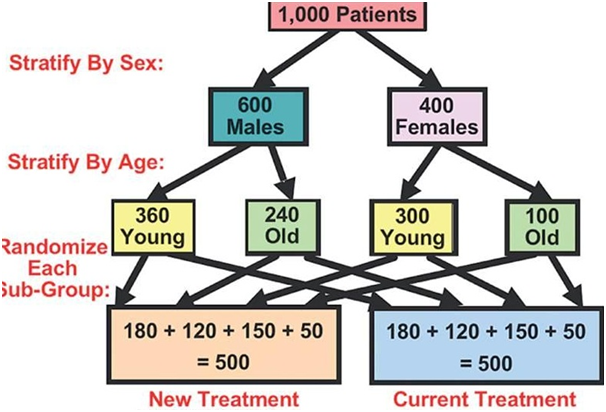
“The block randomization method is designed in order to randomize subjects into groups that result in equal sample sizes.
This method is used to make sure a balance in sample size across groups over time. Blocks are small and balanced with predetermined group assignments, which keeps the numbers of the subjects in each group similar at all times.
The block size is determined by the researcher and should be a multiple of the number of groups (i.e., with two treatment groups, block size of either 4, 6, or 8). Blocks are best used in smaller increments as researchers can more easily control balance.
After block size has been determined, all possible balanced combinations of assignment within the block (i.e., equal number for all groups within the block) must be calculated. Blocks are then randomly chosen to determine the patients’ assignment into the groups.”
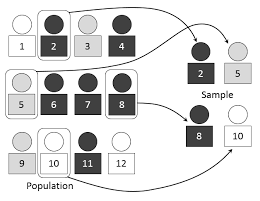
Stratified randomization
“The stratified randomization method addresses the need to control and balance the influence of the covariates.
This method can be used to attain balance among groups in terms of subjects’ baseline characteristics (covariates).
Specific covariates must be identified by the researcher who understands the potential influence each covariate has on the dependent variable.
Stratified randomization can attained by generating a separate block for each combination of covariates, and subjects are assigned to the appropriate block of covariates.
After all subjects have been identified and assigned into blocks, simple randomization is performed within each block in order to assign subjects to one of the groups.
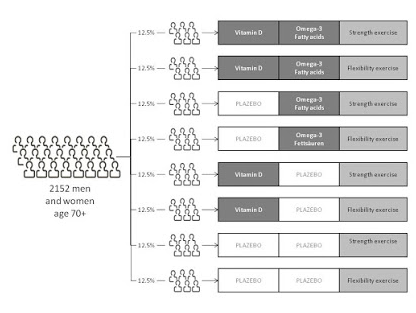
Covariate adaptive randomization
One possible issue with clinical research of small to moderate size is that simple randomization (with or without taking into account the stratification of prognostic variables) can contribute to the imbalance of important covariates between treatment groups.
Covariate imbalances are significant because of their potential to influence the interpretation of a research finding.
Several researchers have proposed covariate adaptive randomisation as a legitimate alternative form of randomization for clinical research.
In covariate adaptive randomization, the sequential assignment of a new participant to a specific treatment group takes into account the specific covariates and previous assignments of participants.
Covariate adaptive randomization uses the minimisation approach by measuring the sample size difference of multiple covariates.
Permuted block randomization
Sometimes, just choosing participants randomly isn’t enough. You might want to balance your participants into groups, or blocks.
Permuted block randomization is a way to randomly allocate a participant to a treatment group, while keeping a balance across treatment groups. Each “block” has a specified number of randomly ordered treatment assignments.”
Eg.. AAABBBBAAABBB
BAABBAAABBAAA
Importance of randomized studies in Health Economics Outcomes Research (HEOR)
Randomized studies are an essential tool in Health Economics and Outcomes Research (HEOR) for evaluating the effectiveness, safety, and cost-effectiveness of healthcare interventions. Read full blog on https://digitalho.com/blog/heor/
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3136079/
https://www.theisn.org/isn-act-toolkit/study-stage-1-design-and-development/randomization
https://www.frontiersin.org/articles/10.3389/fnins.2018.00355/full
https://digitalho.com/blog/heor/